第3节  一元一次不等式（组）

　　6. 5不等式及其性质

　　知识点1：不等式的概念

　　用不等号“<”、“>”、“≤”、“≥”、“≠”表示不等关系的式子，欧博娱乐叫做不等式，如等。

　　例题1.判断下列各式哪些是等式、不等式、既不是等式也不是不等式

　　知识点2：常见的不等号及其含义

　　“≠”读作“不等于”，它表明两个量是不相等的，但不能明确哪个量大，哪个最小

　　读作“大于”，它表明左边的量比右边的量大

　　读作“大于或等于”，它表明左边的晕不小于右边的量

　　读作“小于”它表明左边的量比右边的量小

　　读作“小于或等于”，它表明左边的量不大右边的最

　　例题2.一辆匀速行驶的汽车在l1:20距离A地50千米，要在12:00之前驶过A地，车速应满足什么条件？

　　知识点3：不等式的基本性质

　　不等式的基本性质l：

　　不等式的两边都加上（或减去）同一个整式，不等号的方向不变.

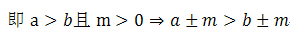
　　不等式的基本性质2：

　　不等式的两边都乘以（或除以）同一个正数，不等号的方向不变.

　　

　　不等式的基本性质3：不等式的两边都乘以（或除以）同一个负数，不等号的方向改变.

　　

　　注意：1 不等式的基本性质2和基本性质3反过来也是成立的．

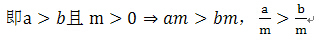
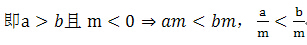
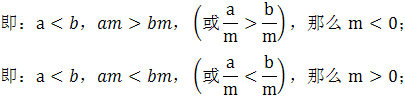
　　知识点4：不等式的基本性质与等式的基本性质的关系

　　1．不等式的三个基本性质与等式的两个基本性质相比较：

　　相同点：不论是等式还是不等式，都可以在它的两边加上（或减去）同一个数或同一个整式．

　　不同点：若是等式，在等式的两边乘以（或除以）同一个正数或同一个负数，等式仍然成立.

　　若是不等式，情况就大不一样：在不等式两边乘以（或除以）同一个正数，不等号方向不变；在不等式两边乘以（或除以）同一个负数，不等号方向一定要改变．

　　2．不等式的三个基本性质是不等式变形的重要依据，性质1、2类似于等式性质，较易掌握，性质3不等号的方向要改变，这是不等式独有的性质，也是初学者易出错的地方，尤其是在不等式两边同乘以（或除以）的数的正负性并不确定，要进行认真仔细的分类讨论，因此要特别注意．

　　6. 6一元一次不等式的解法

　　知识点1.不等式的解的定义

　　能使不等式成立的未知数的值，叫做不等式的解．

　　知识点2：不等式的解集的定义

　　一个含有未知数的不等式的所有解，组成这个不等式的解集

　　6.7一元一次不等式组

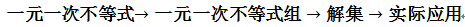
　　知识点1：一元一次不等式组的概念

　　一般地，关于同一个未知数的几个一元一次不等式合在一起，就组成了一个一元一次不等式组

　　都是一元一次不等式组.

　　知识点2：一元一次不等式组的解集的概念

　　一元一次不等式组中各个不等式的解集的公共部分，叫做这个一元一次不等式组的解集．

　　几个一元一次不等式组的解集的公共部分，欧博allbet通常是利用数轴来确定的

　　注意:由两个不等式组成的不等式的解集情况的讨论，

　　特别提醒：如果一元一次不等式组由三个不等式组成，可以先求出两个不等式的公共部分，然后再和第三个不等式求公共部分．

　　知识点3：不等式组的解法

　　解一元一次不等式组的一般步骤：

　　（1）求出不等式组中各个不等式的解集；

　　（2）在数轴上表示各个不等式的解集；

　　（3）确定各个不等式解集的公共部分，就得到这个不等式组的解集．

　　注意：不等式组的解集必须是不等式组里每个不等式解集的公共部分，因此，利用同一数轴表示各不等式的解集，然后正确找到公共部分是解题的关键．

　　知识点4：一元一次不等式组的应用

　　对含有不等关系的应用题，可以考虑通过列不等式或不等式组来解．它的方法、步骤和列方程解应用题类似，列不等式（组）解应用题，求出的通常是一个量的某一个取值范围，但当所求的量必须属于整数集或整数集的某一部分时，求得的解有可能是有限个量，甚至是的值．

　　第四节一次方程组

　　6. 8  一元一次方程

　　知识点1：二元一次方程

　　含有两个未知数，并且所含未知数的项的次数都是1的方程叫二元一次方程

　　注意：

　　知识点2：二元一次方程的解

　　1．二元一次方程的解：使二元一次方程两边的值相等的两个未知数的值，叫做二元一次方程的解．

　　2．二元一次方程的解集：二元一次方程的解有无数个，二元一次方程的解的全体叫做这个二元一次方程的解集．

　　6. 9二元一次方程组及其解法

　　1．定义：两个二元一次方程合在一起，就组成了二元一次方程组

　　注意：二元一次方程组中方程的个数可以超过两个，而且组成方程组的方程不一定都是二元的，也可以是一元的，但要助力方程组中有两个未知数．

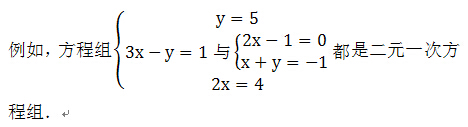
　　2．二元一次方程组的标准形式为

；其中a1、a2中至少有一个不为0，中至少有一个不为0

　　知识点2：二元一次方程组的解

　　1．定义：使二元一次方程组中的两个方程左、右两边的值都相等的两个未知数的值，叫做二元一次方程的解．

　　注意：

　　(1)方程组的解必须用“{”表示．

　　(2)二元一次方程组的解实质上就是组成方程组的两个二元一次方程的公共解．也就是说，方程组的解一定是组成方程组的每个二元一次方程的解，而组成方程组的每个二元一次方程的程的解不一定是方程组的解.

　　2．检验一组数是否为二元一次方程组的解的方法：将这组数值分别代入方程组中的每个方程，当这组数值满足所有方程时，就说这组数值是此方程组的解，否则，就不是．

　　知识点3：用代入消元法解二元一次方程组

　　1．代人消元法：代入消元法简称代入法，它是解二元一次方程组的基本方法之一，是列方程解决实际应用问题的基础．特别是其中的“消元”又体现了数学研究中“化未知为已知”的重要思想，该思想方法不仅在解二元一次方程组中起着重要作用，而且也是后面解二元二次方程组的基本思想方法，所以对此方法要牢固掌握．

　　2．运用代人消元法解方程组的一般步骤为：

　　(1)从方程组中选一个系数较简单的方程，将这个方程中的某个未知数用含有另一个未知数的代数式表示出来：例如ax-y=b，将y用含x的代数式表示出来，就可写成的y=ax-b形式；

　　(2)将y=ax-b代人另一个方程中，从而消去一个未知数y，化二元一次方程组为一元一次方程；

　　(3)解这个一元一次方程，求出未知数x的值；

　　(4)将y=ax-b求得的未知数代入中，求出y的值，得到方程组的解。在具体解题中，还要注意应努力使变形后的方程比较简单和代入后化简比较容易，这样既可以提高解题速度，又可以减少失误．

　　注意：用代入法解二元一次方程组的关键：准确地从方程组的两个方程中选择一个方程变形，对于标准形式的二元一次方程组

，采用的方法是系数比较法，即比较四个整数a1，b1，a2，b2绝对值的大小，选择绝对值最小的一个系数所在的方程变形，若|a1|最小，则选第一个方程；方程选定后，将方程变形为用含一个未知数的代数式表示另一个未知数的形式，变形的目的是为了下一步进行等量代换，即为“代入”作准备．对于二元一次方程的标准形式，只需采用移项和系数化为1两步就行．

　　知识点4：用加减消元法解二元一次方程组

　　1．加减消元法：把两个方程的两边分别加减消去一个未知数的方法，叫加减消元法．

　　2．用加减消元法解方程组的一般步骤：

　　(1)方程组的两个方程中，如果同一个未知数的系数既不互为相反数又不相等，那么就用适当的数乘方程的两边，使同一个未知数的系数互为相反数或相等；

　　(2)把两个方程的两边分别相加或相减，消去一个未知数，得到一个一元一次方程；

　　(3)解这个一元一次方程，求得一个未知数的值；

　　(4)将这个求得的未知数的值代人原方程组中的任意一个方程中，求出另一个未知数的值，并把求得的两个未知数的值用符号“{”联立起来．

　　注意：在运用加减法解二元一次方程组时要注意以下几点：

　　(1)合理选元；

　　(2)当方程中的系数需要扩大（或缩小）若干倍时，要把方程中各项的系数都扩大（或缩小）同样的倍数，不能漏乘，尤其不要漏掉常数项；

　　(3)在加减消元时，要特别注意符号，熟记“减去一个数，等于加上这个数的相反数．”

　　6.10  三元一次方程组及其解法

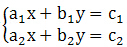
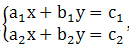
　　知识点：三元一次方程组及其解法

　　1，三元一次方程组：由三个一次方程组成的含有三个未知数的方程组叫做三元一次方程组．

　　2，三元一次方程组的解法：三元一次方程组的解法与二元一次方程组的解法相似，只是要多消一次元，即通过代人法或加减法逐步消元，最后化成一元一次方程进行求解.

　　知识点2：利用线形示意图作为建模策略解决问题

　　列方程（组）解决一些实际问题过程是一个数学化的过程，这个过程中常常需要文字语言、图形语言、符号语言的互相转换，对于工程问题和行程闯题，常用画线段示意图的方式帮助理清数量间的关系．

　　例题2.客车、货车同时从相距180千米的A、B两地出发相向而行．客车从A地到B地后，停留半小时返回A地．货车从B地到A地后停留1小时后返回B地，已知客车速度是36千米／小时，货车速度是24千米／小时，问两车出发后多少小时在返途中相遇？

　　知识点3：利用圆形示意图作为建模策略解决问题

　　圆形示意图常用于解决工程问题，通常用整个圆的面积表示全部工程量1.

　　例题3.将一批会计报表输人电脑，甲单独做需20小时完成，乙单独做需12小时完成，现在先由甲单独做4小时，剩下的部分由甲、乙两人合作完成，甲、乙两人合作的时间是多少？

　　知识点4：利用柱状图作为建模策略解决问题

　　柱状示意图常用于解决商品销售问题，画柱状示意图时可以直接在柱状示意图的长方形区域上写上各个量．